
Analytical Treatment of an Inclusions Embedded in Elastic Media

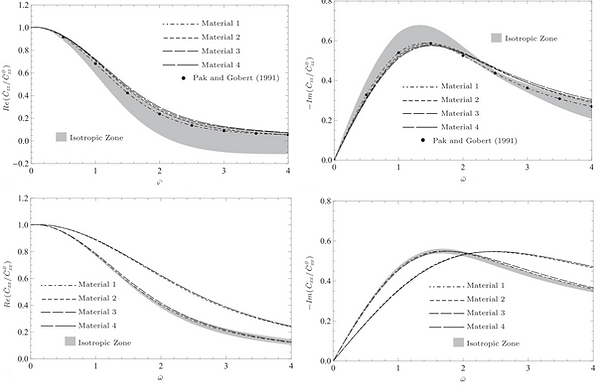
The interaction between a foundation (modeled as a disk) and its surrounding elastic medium (half-space) have been of interest to civil engineers, seismologists, mechanical engineers, and applied mathematicians. For instance, the results of such studies are of great value for better understanding of the behavior of foundations and anchorages under static and dynamic loadings. An important aim of such interaction problems is the determination of the equivalent stiffness of the interacting systems. We try to come up with a simplified model of the associated soil-structure interaction problems. Here, the analytical treatment of normal, rocking, and torsional forced time-harmonic vibrations of a rigid circular disk in a transversely isotropic full-space is studied. A complete discussion on frequently used contact assumptions of adhesive and smooth models is given, and the effects of different contact models on the results of each vibration mode are meticulously discussed. With the aid of appropriate dynamic Green’s functions, the in-plane mode of vibration of the disk is treated analytically. The solution corresponding to each vibration mode is obtained as a well-known Fredholm integral equation. For each vibration mode, the contact stress, the resultant force acting on the disk, and the dimensionless compliance factor are given in terms of the solution of the Fredholm integral equation. For instance, see the normalized vertical (first row) and lateral (second row) compliance versus nondimensional frequency for some transversely isotropic materials. Click here to read more.


Green’s Functions of a Surface-Stiffened Transversely Isotropic Half-Space
Thin films and functionally graded (FG) layers covering the surface of a solid for increasing its thermo-mechanical properties, and application of geotextiles in reinforcing soil strata are some well-known examples which are widely used in various engineering fields. Moreover, corrosion, polishing, and chemical reactions can significantly change the material properties of a thin layer on the surface of a half-space. Therefore, analysis of a coating-substrate system with dissimilar material properties is also of practical interest to material scientists. In most analytical treat of coating-substrate systems, the layer is modeled as a thin plate. In this paper, Green’s functions of a transversely isotropic half- space with surface coating are analytically obtained. The coating layer is modeled as a Kirchhoff thin plate perfectly bonded to the half-space. The point load Green’s functions are composed of a closed-form part (see the solution below) corresponding to the transversely isotropic half- space with kinematic surface constraints in addition to a numerically evaluated part showing the effects of coating flexural stiffness. Click here to read more.




Name, Title
Axisymmetric Circular Indentation of a Half-Space Reinforced by a Buried Elastic Thin Film

